这篇可以看作是JDK源码分析系列–HashMap的下篇。java.util.HashMap.TreeNode是HashMap中非常重要的一个类,主要目的在于:当哈希冲突比较严重的时候,提升HashMap的查询效率。尽管实际用到的概率不高,却占了HashMap篇幅的1/4左右。因此在这写一篇单独分析。
红黑树
三种树对比
首先说二叉树,每个父节点都会最多生出两个子节点,其中,左子节点 < 父节点 < 右子节点,在最好的情况下,二叉树查询的时间复杂度是O(log n),也就是树的层数。在最坏的情况下,即节点的添加顺序是严格递增或严格递减,那二叉树就会退化成链表,时间复杂度为O(n)。
为了解决二叉树偏向一边的情况,引入了平衡二叉树,要求从根节点到任意叶子节点的最短路径之差不大于1。这就保证了平衡二叉树的时间复杂度是O(log n)。但是这种状态是很难保持的,每次插入或移除一个节点,都可能导致性质被破坏,就需要通过自旋的方式来维持平衡。
为了高效的查询,同时不希望像平衡二叉树那样大的开销,于是引入了红黑树。红黑树是有红黑两种颜色的节点组成的二叉树,可以看做是一个不严格的平衡二叉树。
结构
两种不同的插入顺序,得到的数高度不同,但是都遵循左下<右上的标准。
[红黑树插入演示网站](Red/Black Tree Visualization)
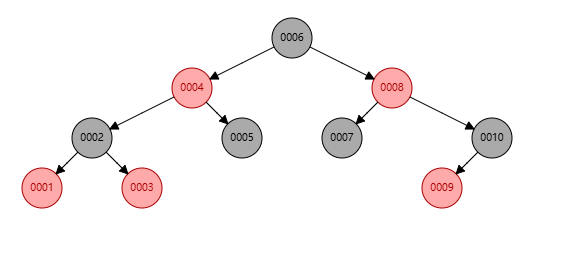
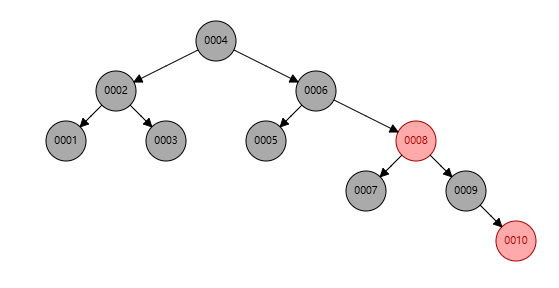
特点
红黑树包括五大特点:
-
每个节点要么是红色,要么是黑色;
-
跟节点是黑色;
-
叶子节点是黑色;
-
红色节点的子节点必须是黑色;
-
从任意节点到任意叶子节点的最短路径上,走过的黑色节点数量都相同
在这样的规则约束下,从根节点到叶子节点的任意路径,节点数最少的情况是都为黑色节点,节点数最多的情况是每个黑色节点的子节点都为红色。由于根节点为黑色,所以后一种的节点数是前一种的两倍。
构造方法
TreeNode只有一个构造方法,内部最终调用的是HashMap.Node的构造方法,创建的是普通节点
1
2
3
| TreeNode(int hash, K key, V val, Node<K,V> next) {
super(hash, key, val, next);
}
|
成员变量
TreeNode
TreeNode新增五个成员变量
当前节点的父节点
当前节点的左子节点
当前节点的右子节点
当前节点的前驱节点
节点颜色,true红色,false黑色
Entry
从LinkedHashMap.Entry继承而来两个成员变量
当前节点的前一个节点
当前节点的后一个节点
Node
从HashMap.Node继承而来的四个成员变量
key的哈希值
key
value
当前节点的后继节点
共有7个节点引用,分为三组:
- prev,next一组,表示链表中的上下节点
- before,after一组,表示插入顺序中的前后节点
- parent,left,right一组,表示树中的父子节点
成员方法
TreeNode有15个成员方法,本文将按照HashMap的put,get,remove,resize的顺序来讲解
putTreeVal方法
在HashMap.putVal方法中,判断数组节点是TreeNode类型,则会调用putTreeVal方法,执行树节点的put逻辑
其中,调用方p是数组节点,this是当前hashMap对象,tab是节点数组,hash、key、value是新节点参数
1
2
| if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
|
整体逻辑如下:
1.找到根节点。如果数组节点不是根节点,则沿着parent指针找到根节点
2.确定新节点在树中的位置,左边还是右边,或者节点已经存在
3.通过判断key的hash值,小于根节点则放在左子节点,大于根节点则放在右子节点
3.1如果hash值相同,而key又不同,则通过compareTo方法来判断大小
3.2如果通过compareTo无法判断大小,则通过find方法在子节点中找到相同的key
3.3如果还是找不到,则通过自定义的方式最终判断出大小
3.4如果判断是在左边,而左节点为null,则放到左子节点上
3.5如果判断是在右边,而右节点为null,则放到右子节点上
3.6如果子节点不为null,则将子节点作为父节点,继续判断,直到子节点为null
3.7由于find方法已执行过一遍(且没查到),所以后面循序不再执行find方法。
4.如果节点已存在,则直接返回
5.如果在左边,判断左子节点是否存在
5.1不存在,则直接放到左子节点,维护双向链表,调整树结构
5.2存在,则回到第二步,继续判断
6.右边同上
源码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
| final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,int h, K k, V v) {
Class<?> kc = null;
boolean searched = false;
TreeNode<K,V> root = (parent != null) ? root() : this;
for (TreeNode<K,V> p = root;;) {
int dir, ph; K pk;
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
return p;
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0) {
if (!searched) {
TreeNode<K,V> q, ch;
searched = true;
if (((ch = p.left) != null &&
(q = ch.find(h, k, kc)) != null) ||
((ch = p.right) != null &&
(q = ch.find(h, k, kc)) != null))
return q;
}
dir = tieBreakOrder(k, pk);
}
TreeNode<K,V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
Node<K,V> xpn = xp.next;
TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);
if (dir <= 0)
xp.left = x;
else
xp.right = x;
xp.next = x;
x.parent = x.prev = xp;
if (xpn != null)
((TreeNode<K,V>)xpn).prev = x;
moveRootToFront(tab, balanceInsertion(root, x));
return null;
}
}
}
|
root方法
在putTreeVal中使用以下语句查找根节点:
1
| TreeNode<K,V> root = (parent != null) ? root() : this;
|
其中,parent即数组节点的父节点,当parent为null时,数组节点就是根节点,否则要调用root方法找到根节点。
源码如下:
1
2
3
4
5
6
7
8
| final TreeNode<K,V> root() {
for (TreeNode<K,V> r = this, p;;) {
if ((p = r.parent) == null)
return r;
r = p;
}
}
|
comparableClassFor和compareComparables是HashMap的成员方法,但是只在TreeNode中用到
HashMap.comparableClassFor方法
用于判断key的类型是否实现了Comparable接口
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| static Class<?> comparableClassFor(Object x) {
if (x instanceof Comparable) {
Class<?> c; Type[] ts, as; Type t; ParameterizedType p;
if ((c = x.getClass()) == String.class)
return c;
if ((ts = c.getGenericInterfaces()) != null) {
for (int i = 0; i < ts.length; ++i) {
if (((t = ts[i]) instanceof ParameterizedType)
&& ((p = (ParameterizedType)t).getRawType() == Comparable.class)
&& (as = p.getActualTypeArguments()) != null
&& as.length == 1 && as[0] == c)
return c;
}
}
}
return null;
}
|
HashMap.compareComparables方法
调用compareTo方法来判断两个key的大小
1
2
3
4
5
6
7
8
9
|
static int compareComparables(Class<?> kc, Object k, Object x) {
return (x == null || x.getClass() != kc ? 0 : ((Comparable)k).compareTo(x));
}
|
这里注意下,x也就是树节点的key,是可能为null的。在HashMap中,key和value都能为null。在HashTable中,key和value都不能为null。
find方法
从根节点的左或者右子节点开始,递归查找,看是否存在相同的key,存在则返回该节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| final TreeNode<K,V> find(int h, Object k, Class<?> kc) {
TreeNode<K,V> p = this;
do {
int ph, dir; K pk;
TreeNode<K,V> pl = p.left, pr = p.right, q;
if ((ph = p.hash) > h)
p = pl;
else if (ph < h)
p = pr;
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
return p;
else if (pl == null)
p = pr;
else if (pr == null)
p = pl;
else if ((kc != null ||
(kc = comparableClassFor(k)) != null) &&
(dir = compareComparables(kc, k, pk)) != 0)
p = (dir < 0) ? pl : pr;
else if ((q = pr.find(h, k, kc)) != null)
return q;
else
p = pl;
} while (p != null);
return null;
}
|
tieBreakOrder方法
比较a和b,是用来打破平衡的终极方法。对于红黑树来说,用什么方法比较key的大小不重要,只要高效且多次比较结果一致即可
1
2
3
4
5
6
7
8
9
10
| static int tieBreakOrder(Object a, Object b) {
int d;
if (a == null || b == null ||
(d = a.getClass().getName().compareTo(b.getClass().getName())) == 0)
d = (System.identityHashCode(a) <= System.identityHashCode(b) ?
-1 : 1);
return d;
}
|
balanceInsertion方法
插入树节点后,通过 balanceInsertion 方法维持树结构的平衡
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
| static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root, TreeNode<K,V> x) {
x.red = true;
for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
if ((xp = x.parent) == null) {
x.red = false;
return x;
}
else if (!xp.red || (xpp = xp.parent) == null)
return root;
if (xp == (xppl = xpp.left)) {
if ((xppr = xpp.right) != null && xppr.red) {
xppr.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
} else {
if (x == xp.right) {
root = rotateLeft(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateRight(root, xpp);
}
}
}
}
else {
if (xppl != null && xppl.red) {
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
} else {
if (x == xp.left) {
root = rotateRight(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateLeft(root, xpp);
}
}
}
}
}
}
|
对于新节点:
1.当父节点是黑色的,插入红色节点,不会有任何影响
2.当父节点是红色,插入红色节点会导致出现两个红节点,树结构被破坏
2.1如果叔节点也是红色,可以将父节点和叔节点都置为黑色,祖父节点置为红色,此时祖父节点往下的部分可以保持平衡。但是祖父节点改为红色可能导致往上的部分结构被破坏,因此需要继续递归处理
2.2如果叔节点为黑色,只能通过旋转保持平衡
2.2.1为右右情况,需要将左边的节点(即祖父节点)按下,右边节点(父节点)提上,交换二者颜色,记为左旋
2.2.2为左左情况,需要将右边的节点(即祖父节点)按下,左边节点(父节点)提上,交换二者颜色,记为右旋
2.2.3为左右情况,需要先左旋,将左边节点按下,右边节点提上,然后按左左情况处理
2.2.4为右左情况,需要先右旋,将右边节点按下,左边节点提上,然后按右右情况处理
规则总结如下:
| 父节点 |
叔节点 |
方向 |
规则 |
| 黑色 |
- |
- |
无 |
| 红色 |
红色 |
- |
父节点和叔节点变成黑色,祖父节点变成红色,将祖父节点变成当前节点,递归处理 |
| 红色 |
黑色 |
右右 |
先左旋,再交换颜色 |
| 红色 |
黑色 |
左左 |
先右旋,再交换颜色 |
| 红色 |
黑色 |
左右 |
先左旋,再右旋,再交换颜色 |
| 红色 |
黑色 |
右左 |
先右旋,再左旋,再交换颜色 |
rotateLeft方法
左旋方法,在balanceInsertion中调用了两次,涉及到左右(<)和右右(\)的情况
1
| root = rotateLeft(root, x = xp);
|
1
| root = rotateLeft(root, xpp);
|
主要作用是:按下p节点,使p作为r(p的右子节点)的左子节点,r作为p的父节点。pp作为r的父节点。rl作为p的右子节点
源码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root, TreeNode<K,V> p) {
TreeNode<K,V> r, pp, rl;
if (p != null && (r = p.right) != null) {
if ((rl = p.right = r.left) != null)
rl.parent = p;
if ((pp = r.parent = p.parent) == null)
(root = r).red = false;
else if (pp.left == p)
pp.left = r;
else
pp.right = r;
r.left = p;
p.parent = r;
}
return root;
}
|
rotateRight方法
右旋同理,在balanceInsertion中调用了两次,涉及到右左(>)和左左(/)的情况
1
| root = rotateRight(root, x = xp);
|
1
| root = rotateRight(root, xpp);
|
主要作用是:按下p节点,使p作为l(p的左子节点)的右子节点,l作为p的父节点。pp作为l的父节点。lr作为p的左子节点
源码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root, TreeNode<K,V> p) {
TreeNode<K,V> l, pp, lr;
if (p != null && (l = p.left) != null) {
if ((lr = p.left = l.right) != null)
lr.parent = p;
if ((pp = l.parent = p.parent) == null)
(root = l).red = false;
else if (pp.right == p)
pp.right = l;
else
pp.left = l;
l.right = p;
p.parent = l;
}
return root;
}
|
moveRootToFront方法
当红黑树增加节点、移除节点或者树化后,根节点可能已经不是数组桶中的第一个节点
moveRootToFront 方法作用是:如果root节点不是数组节点,则将root节点移动到双向链表头部,并作为新的数组节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| static <K,V> void moveRootToFront(Node<K,V>[] tab, TreeNode<K,V> root) {
int n;
if (root != null && tab != null && (n = tab.length) > 0) {
int index = (n - 1) & root.hash;
TreeNode<K,V> first = (TreeNode<K,V>)tab[index];
if (root != first) {
Node<K,V> rn;
tab[index] = root;
TreeNode<K,V> rp = root.prev;
if ((rn = root.next) != null)
((TreeNode<K,V>)rn).prev = rp;
if (rp != null)
rp.next = rn;
if (first != null)
first.prev = root;
root.next = first;
root.prev = null;
}
assert checkInvariants(root);
}
}
|
checkInvariants方法
用于验证红黑树结构是否正确。由于该方法调用时使用assert关键字,所以只有当启动时加上-ea参数才生效,默认不生效。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| static <K,V> boolean checkInvariants(TreeNode<K,V> t) {
TreeNode<K,V> tp = t.parent, tl = t.left, tr = t.right,
tb = t.prev, tn = (TreeNode<K,V>)t.next;
if (tb != null && tb.next != t)
return false;
if (tn != null && tn.prev != t)
return false;
if (tp != null && t != tp.left && t != tp.right)
return false;
if (tl != null && (tl.parent != t || tl.hash > t.hash))
return false;
if (tr != null && (tr.parent != t || tr.hash < t.hash))
return false;
if (t.red && tl != null && tl.red && tr != null && tr.red)
return false;
if (tl != null && !checkInvariants(tl))
return false;
if (tr != null && !checkInvariants(tr))
return false;
return true;
}
|
getTreeNode方法
在HashMap.getNode方法中,判断数组节点是TreeNode类型,则会调用getTreeNode方法,执行树节点的get逻辑
其中,调用方node是数组节点,根据hash和查找
1
2
| if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
|
先判断数组节点是不是根节点,如果不是,则通过root方法找到根节点。之后调用find方法,从根节点开始查找,找不到则返回null
1
2
3
4
| final TreeNode<K,V> getTreeNode(int h, Object k) {
return ((parent != null) ? root() : this).find(h, k, null);
}
|
removeTreeNode方法
在HashMap.removeNode方法中,判断数组节点是TreeNode类型,则会调用removeTreeNode方法,执行树节点的remove逻辑
其中,调用方node是要删除的节点,this是当前hashMap对象,tab是节点数组,movable为true会执行moveRootToFront方法
1
2
| if (node instanceof TreeNode)
((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
|
removeTreeNode方法移除节点p按两部分进行:双向链表和红黑树。两部分互不影响
-
先处理双向链表
1.如果p是头节点,则将p的后继节点作为头节点
2.如果p是中间节点,则将p的前驱节点指向后继节点
-
再处理红黑树
1.如果节点数 <= 6,执行去树化操作,不再需要后续的红黑树处理
2.如果节点数 >6,按p是否存在子节点,分四种情况讨论
2.1没有子节点。这种情况最简单,直接移除p即可
2.2只有左子节点。移除p,用左子节点作为替换节点
2.3只有右子节点。移除p,用右子节点作为替换节点
2.4左右节点都有
2.4.1找到仅大于p的节点s(也就是p的右子节点的最左节点),交换s和p,分三步进行
2.4.1.1交换s和p的颜色
2.4.1.2将p的父节点、左子节点、右子节点作为s的父节点、左子节点、右子节点
2.4.1.3将s的父节点、右子节点作为p的父节点、右子节点(s没有左子节点)
2.4.2交换后,s节点的位置没有问题,p节点不符合要求,删除p节点即可
2.4.3如果p存在右子节点,则将右子节点作为替换节点
3.移除p后,替换节点有两种情况
3.1存在替换节点,连接替换节点和p的父节点
3.2不存在替换节点,使p的父节点的子节点指向null
4.p是黑色节点,则需要调整红黑树结构
5.将根节点移动到数组上
源码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
| final void removeTreeNode(HashMap<K,V> map, Node<K,V>[] tab, boolean movable) {
int n;
if (tab == null || (n = tab.length) == 0)
return;
int index = (n - 1) & hash;
TreeNode<K,V> first = (TreeNode<K,V>)tab[index], root = first, rl;
TreeNode<K,V> succ = (TreeNode<K,V>)next, pred = prev;
if (pred == null)
tab[index] = first = succ;
else
pred.next = succ;
if (succ != null)
succ.prev = pred;
if (first == null)
return;
if (root.parent != null)
root = root.root();
if (root == null || root.right == null ||
(rl = root.left) == null || rl.left == null) {
tab[index] = first.untreeify(map);
return;
}
TreeNode<K,V> p = this, pl = left, pr = right, replacement;
if (pl != null && pr != null) {
TreeNode<K,V> s = pr, sl;
while ((sl = s.left) != null)
s = sl;
boolean c = s.red; s.red = p.red; p.red = c;
TreeNode<K,V> sr = s.right;
TreeNode<K,V> pp = p.parent;
if (s == pr) {
p.parent = s;
s.right = p;
}
else {
TreeNode<K,V> sp = s.parent;
if ((p.parent = sp) != null) {
if (s == sp.left)
sp.left = p;
else
sp.right = p;
}
if ((s.right = pr) != null)
pr.parent = s;
}
p.left = null;
if ((p.right = sr) != null)
sr.parent = p;
if ((s.left = pl) != null)
pl.parent = s;
if ((s.parent = pp) == null)
root = s;
else if (p == pp.left)
pp.left = s;
else
pp.right = s;
if (sr != null)
replacement = sr;
else
replacement = p;
}
else if (pl != null)
replacement = pl;
else if (pr != null)
replacement = pr;
else
replacement = p;
if (replacement != p) {
TreeNode<K,V> pp = replacement.parent = p.parent;
if (pp == null)
root = replacement;
else if (p == pp.left)
pp.left = replacement;
else
pp.right = replacement;
p.left = p.right = p.parent = null;
}
TreeNode<K,V> r = p.red ? root : balanceDeletion(root, replacement);
if (replacement == p) {
TreeNode<K,V> pp = p.parent;
p.parent = null;
if (pp != null) {
if (p == pp.left)
pp.left = null;
else if (p == pp.right)
pp.right = null;
}
}
if (movable)
moveRootToFront(tab, r);
}
|
balanceDeletion方法
balanceDeletion方法只在removeTreeNode方法中唯一调用。由上面的分析可知,调用者p一定为黑色节点,x为替代节点,有四种可能:p,pr,pl,sr。p被移除后,从x节点开始到任意叶子节点的黑色节点数,一定比从x的兄弟节点开始到叶子节点的黑色节点数少1。
balanceDeletion方法内是一个for循环,只能从内部跳出。循环体共分为五个if分支:
- x节点为空或者x节点为根节点,返回根节点。
- x的父节点为空,说明x节点就是根节点,将x节点置为黑色,返回x。
- x节点不是根节点,且为红色,则将x节点置为黑色,就能保证x分支的黑色节点数符合要求,返回根节点。
- x节点不是根节点,且为黑色,且为左子节点。
- x节点不是根节点,且为黑色,且为右子节点。
其中,1、2、3都是方法的结束条件,在若干次循环后,总能进入1、2、3分支。4、5是对称分支,该分支会通过自旋的方式调整平衡,并最后会使x指向xp或者指向root,完成向1、2、3分支的靠拢。
由于x分支比兄弟分支黑色节点数少1,所以4、5平衡的方式有两种:
- 如果兄弟分支有红色节点,则将该节点旋转移动到x分支,并置为黑色,使x分支黑色节点数+1。
- 如果兄弟分支没有红色节点,则将黑色节点置为红色,使兄弟分支黑色节点数-1。但这样x分支又比堂兄弟分支数量少1,因此使x指向xp,继续下一个循环。
源码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
| static <K,V> TreeNode<K,V> balanceDeletion(TreeNode<K,V> root, TreeNode<K,V> x) {
for (TreeNode<K,V> xp, xpl, xpr;;) {
if (x == null || x == root)
return root;
else if ((xp = x.parent) == null) {
x.red = false;
return x;
}
else if (x.red) {
x.red = false;
return root;
}
else if ((xpl = xp.left) == x) {
if ((xpr = xp.right) != null && xpr.red) {
xpr.red = false;
xp.red = true;
root = rotateLeft(root, xp);
xpr = (xp = x.parent) == null ? null : xp.right;
}
if (xpr == null)
x = xp;
else {
TreeNode<K,V> sl = xpr.left, sr = xpr.right;
if ((sr == null || !sr.red) &&
(sl == null || !sl.red)) {
xpr.red = true;
x = xp;
}
else {
if (sr == null || !sr.red) {
if (sl != null)
sl.red = false;
xpr.red = true;
root = rotateRight(root, xpr);
xpr = (xp = x.parent) == null ?
null : xp.right;
}
if (xpr != null) {
xpr.red = (xp == null) ? false : xp.red;
if ((sr = xpr.right) != null)
sr.red = false;
}
if (xp != null) {
xp.red = false;
root = rotateLeft(root, xp);
}
x = root;
}
}
}
else {
if (xpl != null && xpl.red) {
xpl.red = false;
xp.red = true;
root = rotateRight(root, xp);
xpl = (xp = x.parent) == null ? null : xp.left;
}
if (xpl == null)
x = xp;
else {
TreeNode<K,V> sl = xpl.left, sr = xpl.right;
if ((sl == null || !sl.red) &&
(sr == null || !sr.red)) {
xpl.red = true;
x = xp;
}
else {
if (sl == null || !sl.red) {
if (sr != null)
sr.red = false;
xpl.red = true;
root = rotateLeft(root, xpl);
xpl = (xp = x.parent) == null ?
null : xp.left;
}
if (xpl != null) {
xpl.red = (xp == null) ? false : xp.red;
if ((sl = xpl.left) != null)
sl.red = false;
}
if (xp != null) {
xp.red = false;
root = rotateRight(root, xp);
}
x = root;
}
}
}
}
}
|
split方法
在HashMap.resize方法中,判断数组节点是树节点时,会调用红黑树的拆分方法split。
其中,调用方为数组节点,this是当前hashMap对象,newTab是扩容后的数组,j是e在旧数组上的位置,oldCap是旧数组长度。
1
2
| else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
|
split与resize方法中拆分链表的逻辑类似
- 将红黑树所在链表按在新数组中的位置拆分成两条
- 低位链表放置在原来数组位置上,高位链表放置在数组右移oldCap位置上
- 如果链表长度<=6,则将红黑树结构转换成链表。否则重新维护红黑树结构
源码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
| final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) {
TreeNode<K,V> b = this;
TreeNode<K,V> loHead = null, loTail = null;
TreeNode<K,V> hiHead = null, hiTail = null;
int lc = 0, hc = 0;
for (TreeNode<K,V> e = b, next; e != null; e = next) {
next = (TreeNode<K,V>)e.next;
e.next = null;
if ((e.hash & bit) == 0) {
if ((e.prev = loTail) == null)
loHead = e;
else
loTail.next = e;
loTail = e;
++lc;
}
else {
if ((e.prev = hiTail) == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
++hc;
}
}
if (loHead != null) {
if (lc <= UNTREEIFY_THRESHOLD)
tab[index] = loHead.untreeify(map);
else {
tab[index] = loHead;
if (hiHead != null)
loHead.treeify(tab);
}
}
if (hiHead != null) {
if (hc <= UNTREEIFY_THRESHOLD)
tab[index + bit] = hiHead.untreeify(map);
else {
tab[index + bit] = hiHead;
if (loHead != null)
hiHead.treeify(tab);
}
}
}
|
问题:红黑树拆分实质是对链表的拆分,原有的树结构去哪了?
-
对于长度<=6的链表,会调用untreeify方法创建新链表,并放置到数组上。原树结构的节点不再被引用,会被虚拟机回收;
-
对于长度>6的链表,会调用treeify方法重新梳理树结构,原有的树引用(parent, left, right)会被重置。
treeify方法
当链表转红黑树或红黑树拆分后,会执行treeify方法,根据链表维护红黑树结构。
其中,调用方loHead是链表头结点
源码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| final void treeify(Node<K,V>[] tab) {
TreeNode<K,V> root = null;
for (TreeNode<K,V> x = this, next; x != null; x = next) {
next = (TreeNode<K,V>)x.next;
x.left = x.right = null;
if (root == null) {
x.parent = null;
x.red = false;
root = x;
}
else {
K k = x.key;
int h = x.hash;
Class<?> kc = null;
for (TreeNode<K,V> p = root;;) {
int dir, ph;
K pk = p.key;
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0)
dir = tieBreakOrder(k, pk);
TreeNode<K,V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
x.parent = xp;
if (dir <= 0)
xp.left = x;
else
xp.right = x;
root = balanceInsertion(root, x);
break;
}
}
}
}
moveRootToFront(tab, root);
}
|
untreeify方法
当树节点<=6时,会调用untreeify方法,执行红黑树转链表操作
其中,调用方loHead是链表头节点,会返回一个新链表
1
| tab[index] = loHead.untreeify(map);
|
源码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| final Node<K,V> untreeify(HashMap<K,V> map) {
Node<K,V> hd = null, tl = null;
for (Node<K,V> q = this; q != null; q = q.next) {
Node<K,V> p = map.replacementNode(q, null);
if (tl == null)
hd = p;
else
tl.next = p;
tl = p;
}
return hd;
}
|
参考资料
- HashMap中的TreeNode
- TreeNode内部类源码分析




